After looking at the need for global equal area projections and a number of different possible projections, we shall now look at the pseudo-cylindrical options. There are a lot more of these, so we cover them in an article of their own.
Pseudo-cylindrical projections are similar to cylindrical projections, but the central meridian is the only meridian that is straight. All other meridians are curved. These are all mathematical projections, with the choice of curve producing different effects. As with the equal area cylindrical projections, the spacings of the parallels (lines of constant latitude) for all of the equal area pseudo-cylindrical projections are chosen to ensure that the equal area property is maintained.
In the following listing, the “Meridians are:” entry does not refer to the central meridian which is always straight for these projections.
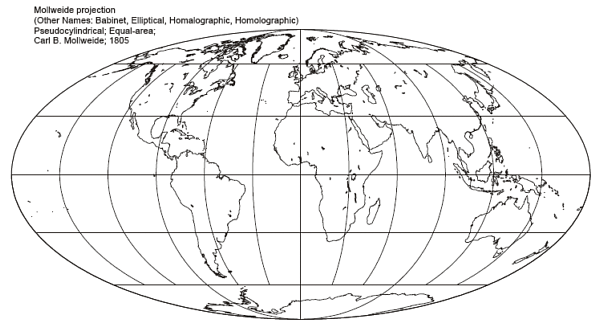
Mollweide
Also known as: Babinet, Elliptical, Homolographic, Homalographic.
Meridians are: Equally spaced elliptical arcs.
Shape and direction are not distorted at the intersection of the central meridian and latitudes 40deg44min north and south. Shape is increasingly distorted away from these points.
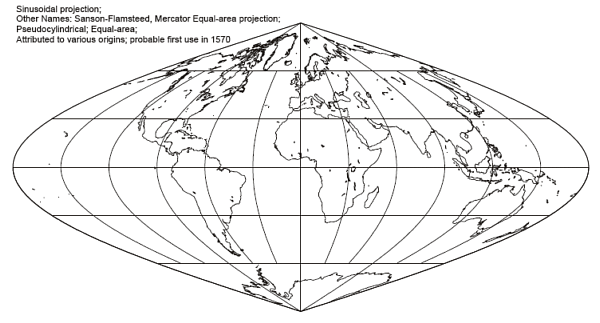
Sinusoidal
Also known as: Sanson-Flamsteed
Meridians are: Sine functions
Shape and angles are correct along the central meridian and equator. However, the distortion increases away from the central meridian, and can be high near the edges. The low level of central distortion is a useful characteristic, but the high levels of distortion near the edges count against this projection.
This projection is often interrupted in order to reduce the distortion, but this is not currently practical for web mapping applications.
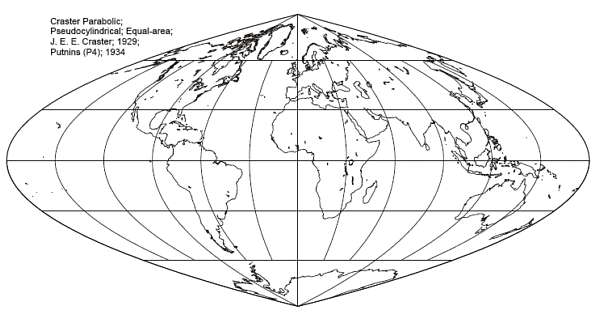
Craster Parabolic
Also known as: Putnins P4
Meridians are: Parabolas
Shape and direction are not distorted at the intersection of the central meridian and 36deg46min north and south. Shape is increasingly distorted away from these points, and is greatest for the outer meridians and near the poles.
This is another projection which is often interrupted in order to reduce the distortion.
The Eckert Projections
Eckert produced a series of six projections. Three of these, Eckert II, IV, and VI are equal area pseudocylindrical projections.
Eckert II is an angular hexagonal shape with discontinuous meridians at the equator. This is considered a novelty projection with few if any real world applications.
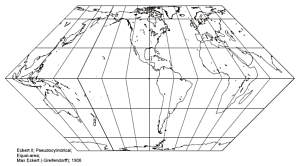
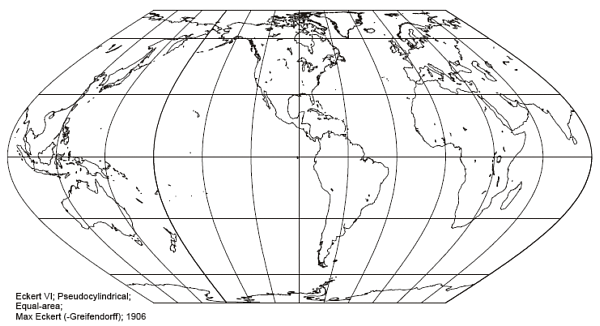
Eckert IV has meridians which are elliptical arcs, whilst Eckert VI has sinusoidal meridians.
Local angles and shape are correct at the intersection of the central meridian with 40deg30min north and south for Eckert IV, and 49deg16min for Eckert VI.
Eckert IV stretches shapes and scale by 40% in the north-south direction, along the equator. This stretching reduces to zero at 40deg30min north and south, and becomes a compression towards the poles.
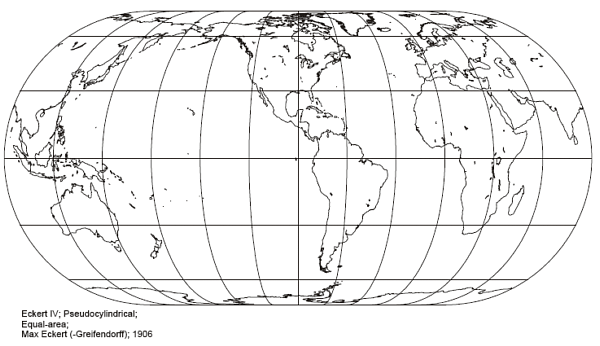
Eckert VI stretches shapes and scale by 29% in the north-south direction, along the equator. This stretching reduces to zero at 49deg16min north and south, and becomes a compression towards the poles.
Hence Eckert VI appears to have less distortion in the lower and mid latitudes, but distortion appears visually greater near the eastern and western edges.
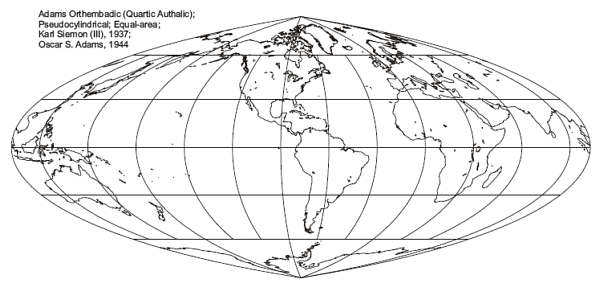
Quartic Authalic
Also known as: Adams Orthembadic
Meridians are: Quartic (fourth order polynomials)
Direction and shape are generally distorted, but scale is constant along the equator and any given latitude.
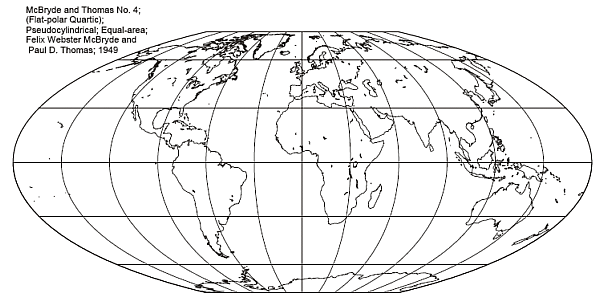
McBryde-Thomas Flat Polar Quartic
Meridians are: Quartics (based on the Quartic Authalic)
Shapes are only free of distortion at the intersection between the central meridian and latitudes 33deg45 north and south. Shapes are stretched in the north-south direction between these points. Shapes are squashed in a north-south direction towards the poles.
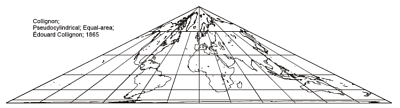
Collignon
Meridians are: Straight lines
A pseudo-cylindrical projection can have straight meridians, as demonstrated by the Collignon projection. This results in a triangle or a diamond shape.
The Collignon projection is usually classified as a novelty projection, although in recent years it has found use in cosmology for storing and displaying cosmic background data.
Conclusions
The Collignon and Eckert II projections can be quickly dismissed as novelty projections. The triangular Collignon is difficult to read and shows extreme shape distortion. The Eckert II and diamond Collignon (not illustrated) also show unnatural discontinuities at the equator.
All of the remaining projections are suitable for the display of equal area maps where data density, area, and/or relative distributions are important. The exact choice will depend on the acceptable amount and position of the inevitable distortion. This is in some degrees subjective.
Combined with the projections identified in part 2 of this article, here are the equal area projections which are deemed suitable for web mapping of global data:
- Azimuthal
- Hammer
- Cylindrical
- Berhmann
- Pseudo-cylindrical
- Craster Parabolic
- Eckert IV
- Eckert VI
- McBryde-Thomas Flat Polar
- Mollweide
- Quartic Authalic
- Sinusoidal
Although regional projections were not the subject of this article, the Albers Conic and Lambert Azimuthal Equal Area projections were identified as suitable for regional equal area maps.
All of these projections are supported by ESRI and the Proj.4 library.
In the next article in this series, I shall create a functioning web map application that allows users to plot their data on one of these projections.
Acknowledgments
The projection images are public domain images produced by Paul B Anderson.