In the first part of this article, I argued against the use of Mercator and Equirectangular projections for web maps showing global data distributions and areas. Instead, an equal area projection is more appropriate because it preserves relative areas and data densities.
In the final two parts, I shall look at some possible equal area projections that might be useful for an online mapping application. I start by looking at conic, pseudo-conic, azimuthal, and cylindrical projections. Tomorrow, in the final part of this article, I shall look at pseudo-cylindrical projections.
Criteria
In our search for a suitable equal area projection, I have identified a number of criteria. The projection should:
- Preserve relative area sizes
- Minimize shape distortion as much as possible
- In many cases this will be subjective. It is likely we will identify a number of projections with different shape distortion patterns
- Be practical with widespread support
- I have deemed a projection “practical” if it has support from ESRI and the Proj.4 library. ESRI are the largest vendor of GIS products; and the proj.4 library is by far the most popular open source projection library.
- Have a global scope
- Be continuous
- Some projections are interrupted (split) to help minimize shape distortions. These interruptions are difficult for today’s software to handle. There is also a tendency for readers to misinterpret the interruptions as ocean.
Conic Projections
Conic projections can be used to create equal area projections, but they only cover a region.
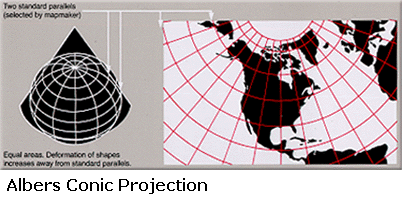
Albers Conic
The Albers Conic projection is one of the most common equal area conic projections. Although it is limited to small countries and regions, it is included here for completeness.
The Albers projection is defined by two standard parallels. Although shape and linear scale are not perfectly preserved, their distortion between the parallels is minimized. Useful for mapping small countries and regions in the mid-latitudes, but works better for east-west areas rather than north-south areas.
Pseudo-Conic Projections
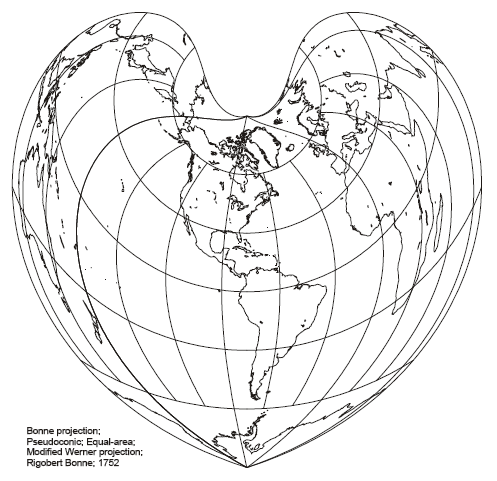
Bonne & Werner Projections
The Bonne projection is a pseudo-conic projection, with parallels that are equally spaced concentric circular arcs. Direction, scale, and shape fidelity are true along the central meridian and standard parallel, but distortion increases away from these lines.
The Werner Projection is a special case where the aspect (center) is positioned over the pole. If the aspect is located over the equator, a Sinusoidal Pseudo-Cylindrical projection results (see tomorrow’s article on pseudo-cylindrical projections).
The Bonne projection is usually only used for continental maps due to distortion near the edges. It was very popular during the 19th and early 20th centuries for large atlas maps (eg. of Asia), but has since fallen out of favor.

Azimuthal Projections
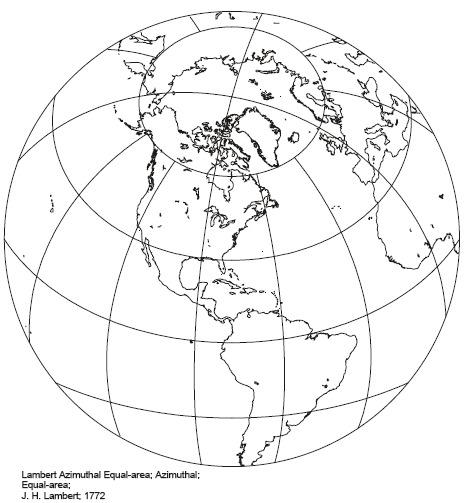
Lambert Azimuthal Equal Area
This projection was derived by Lambert using calculus to guarantee preservation of area. As well as preserving area, direction is preserved from the central location. Distortion increases away from the central location, with contraction in the radial direction and expansion in the transverse direction.
The Lambert Azimuthal Equal Area projection is limited to only one hemisphere at a time, and is included here for completeness. It is particularly useful for large roughly symmetrical areas, and is often used for the polar regions.
The Lambert Azimuthal Equal Area projection also has non-cartographic applications in structural geology, where it is used to analyse the relationships between different orientations.
Hammer
Also known as the Hammer-Aitoff projection, but not to be confused with the Aitoff projection which is NOT an equal area projection. Historically, confusion was fed by Hammer being inspired by Aitoff’s projection and giving prominent credit to Aitoff in the paper that formally described the Hammer Projection. Today, the Hammer is often known as the “Hammer-Aitoff” which recognizes this historical precedence but only continues the confusion.
The Hammer is a global projection that is a modification of the Lambert Azimuthal Equal Area Projection. The equator is the only straight parallel. All other parallels are complex curves. Angles are only true where the equator and the central meridian intersect.

Cylindrical Projections
Cylindrical projections have straight meridians. The parallels are also straight, and perpendicular to the meridians. Cylindrical projections vary according to how the parallels are spaced. It is possible to create an equal area projection by moving high latitude parallels closer together relative to the equatorial parallels. This relationship is defined mathematically. Specific equal area cylindrical projections are also defined by a Standard Parallel – the latitude where x,y scaling is equal and shape is preserved.
Behrmann Equal Area Cylindrical
This is an equal area cylindrical projection. Standard parallels are at 30 degrees north and south.

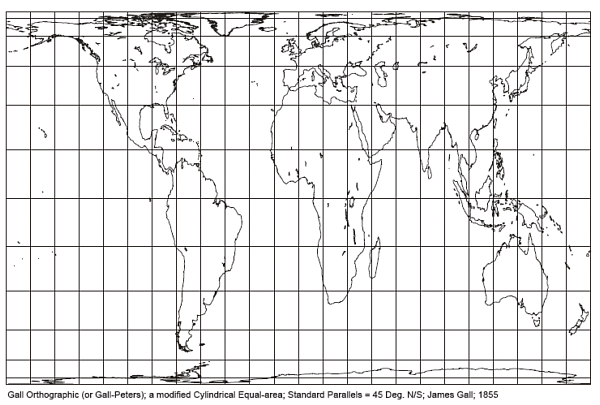
Gall-Peters
Also known as: Gall Orthographic, Peters
Another equal area cylindrical projection is the notorious Gall-Peters projection. This is an orthographic cylindrical projection with standard parallels of 45 degrees north and south. It was originally invented by Gall in 1855, but remained in obscurity until Arno Peters (apparently independently) devised a virtually identical projection (standard parallel of 44.138) in
1967. The Peters Projection was intended to show a more representative map of the relative area of the equatorial and third world countries compared to the first world. The few professional cartographers who commented, were very critical. Despite this, it has seen widespread use by various socially concerned agencies including the United Methodist Church, the Vatican, the World Council of Churches, and various UN agencies. I remember it making regular appearances in British high schools during the 1980s. At a school level, it probably had “shock value” indicating the relative size of Africa to Europe. Some of the critics probably disliked the underlying politics, although it also has practical geometric problems. The Gall-Peters projection is an equal area projection, but has a lot more shape distortion than most equal area projections. As pointed out by its critics, the most visible distortion is at lower latitudes – exactly where it is meant to be most representative.
Conclusions
I have looked at a number of different equal area projections. In our search for a global projection, we can quickly discard the Albers Conic and Lambert Azimuthal Equal Area projections. Neither projection has a global scope, but I included them in this survey because they are very useful equal area projections for regional areas.
The Bonne and Werner projections are interesting looking projections, but they are probably too unfamiliar for modern map readers. They also have high levels of shape distortion at their edges.
The Gall-Peters has received a lot of publicity for solving the very problem that we are looking at. However, the equatorial shape distortion is extreme; and the Behrmann is a very similar projection but with much lower levels of distortion.
This leaves the Hammer and Behrmann projections as candidates for our global maps.
In the final part of this article, I shall look at the Pseudo-Cylindrical projections.
Acknowledgments
The Albers projection image is licensed under the Creative Commons license, and available from the Wikimedia Commons.
The remaining projection images are public domain images produced by Paul B Anderson.